บทความนี้ย้ายบล๊อกมาจาก nartra.blogspot.com กำลังรีไรท์
DFS & BFS
วิธีการค้นหาข้อมูลใน Tree (โครงสร้างข้อมูลแบบ Tree คืออะไรถ้ายังไม่รู้ให้ไปอ่านก่อนที่ label/Tree) สำหรับ Tree ทุกรูปแบบ ใช้ 2 วิธีนี้ได้หมด
เรียกว่าเป็นวิธีมาตราฐานของการ Tree Searching กันเลยถึงแม้ว่าประสิทธิภาพมันจะไม่ค่อยดีเท่าไหร่ก็ตามล่ะนะ
Depth-First Search
หรือ "การค้นหาตามแนวลึก" วิธีการคือพุ่งตรงดึงเข้าไปก่อนเลย สุดทางแล้วค่อยถอยกลับมาแล้วหาทางใหม่ลองไปเรื่อยๆ
ถ้าเราจะเรียบเทียบกับรูปข้างบน เราต้องการจะหาคนๆ หนึ่งซึ่งเป็นเพื่อนเราที่อยู่กลางฝูงชนมากมาย เราก็จะทำแบบนี้
หาแบบเป็นแนวตรงดึงเข้าไปเลย ซึ่งถ้าไม่เจอเราก็ลองหาทางใหม่ดู
ทีนี้ลองมาดูโครงสร้างแบบ Tree จริงๆ กันบ้าง
ป.ล.ขอยกตัวอย่างด้วย Binary Tree เพราะมันง่ายดี
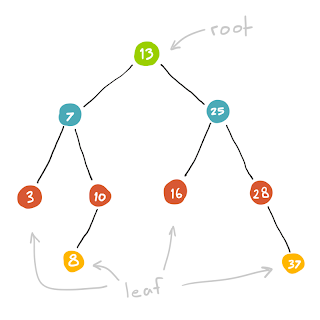 |
| เริ่มต้นด้วย Tree 1 ตัว |
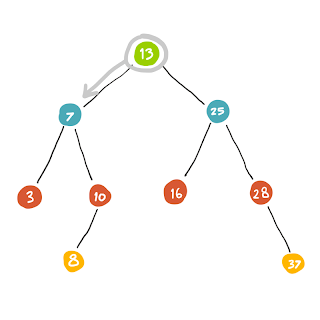 |
| หาจาก root เป็นลำดับแรก เมื่อยังหาไม่เจอ เราก็จะทำกาเขยิบไปตัวต่อไปซึ่งก็คือ child ของมันสักตัวนึงที่เรายังไม่เคยผ่านมากก่อน |
 |
| (13) ผ่านมาแล้ว จึงทำเครื่องหมายให้่รู้ไว้ด้วย ในตัวถัดไปก็ทำแบบเดียวกันคือถ้ายังไม่เจอก็ลงไปหาตัวต่อไปลึกๆ ก่อน |
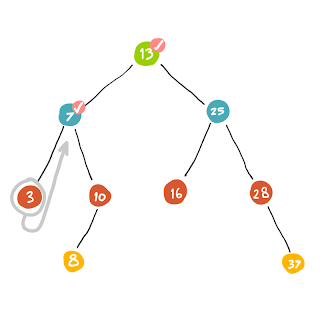 |
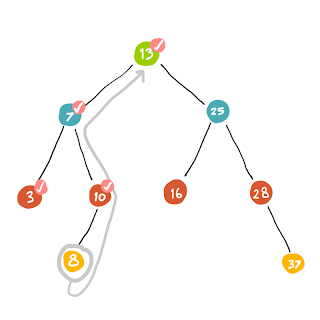
| ทีนี้พอถึง (3) เมื่อเราไปต่อไม่ได้แล้วก็จำเป็นต้องถอยกลับ |
 |
| เราถอยกลับมาที่ (7) ซึ่ง child ของ (7) มี (3) และ (10) ... สำหรับ (3) นั้นเพิ่งเดินผ่านมันมา เราก็เลยเลือก (10) เป็นตัวถัดไปแทน |
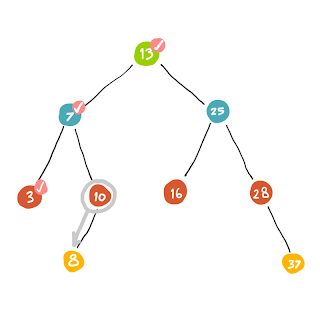 |
| ลงไปที่ (8) |
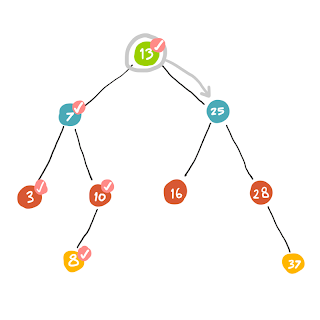 |
| เมื่อเรามาถึง root .. ฝั่งซ้ายนั้นเราทำการค้นหาไปหมดแล้ว ลำดับต่อไปก็เลยจะไปหาทางขวาแทน (ซึ่งทางขวาก็ทำเหมือนฝั่งซ้ายนั่นแล) |
Breadth-First Search
หรือ "การค้นหาตามแนวกว้าง" วิธีนี้เป็นการมองหาแบบกว้างๆ ทีละชั้น หาไล่ไปเรื่อยๆ ถ้ารอบตัวชั้นแรกยังหาไม่เจอ ก็ไปหาชั้นที่อยู่ถัดไปแบบนี้ไปเรื่อยๆ
เราจะแบ่ง Tree ออกเป็นชั้นๆ (หรือเรียกว่า Level) เริ่มตั้งแต่ level 0, 1, 2, ... n
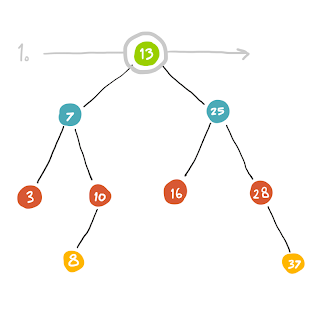 |
| การหาครั้งที่ 1 นั้นจะหาตัวที่อยู่ชั้นบนสุด |
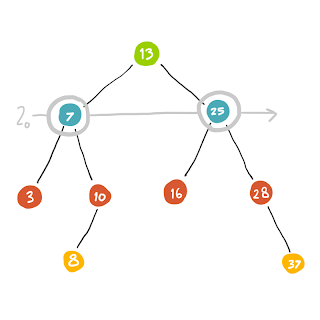 |
| แล้วก็หา Node ในชั้นต่อไปเรื่อยๆ |
 |
| เรื่อยๆ |
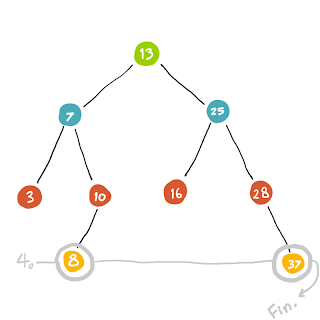 |
| เรื่อยๆ ..จนหมดนะ |
In Action
โปรเจคนี้เป็น workshop ที่จะให้อ่าน input ซึ่งบรรทัดแรกจะเป็น data ที่ใส่เข้าไปใน Tree เป็นค่าตั้งต้น (วิธีการเขียน Tree และการ insert ข้อมูลใส่เข้าไปหาอ่านได้ที่ ตัวอย่างคลาส Tree แบบง่าย)
ส่วนในบรรทัดต่อไป (มีอีกกี่บรรทัดก็ได้) จะเป็นคำสั่งให้ทำการ search ข้อมูลใน Tree ในรูปแบบ BFS และ DFS เช่นในบรรทัดแรก BFS(28)หมายความว่าให้หา (28) ด้วยวิธีแบบ BFS
13 7 25 3 10 16 28 8 37
BFS(28)
DFS(28)
BFS(90) <-- กรณีนี้จะได้ผลเป็นหาไม่เจอ
เวลาเอาไปรันก็จะได้ผล output ประมาณนี้
Found: 28 Sum: 74 Path: 13 7 25 3 10 16 Found: 28 Sum: 82 Path: 13 7 3 10 8 25 16 Not Found: 90 Sum: 0
Sum และ Path จะเป็นตัวบอกว่า Node ที่เราหาเป็นทางผ่านกว่าจะเจอผลลัพท์มีค่ารวมและผ่าน Node ตัวไหนมาแล้วบ้าง
method BFS
public void BFS(int value) {
int sum = 0;
ArrayList<Node> path = new ArrayList<Node>();
Queue<Node> next = new LinkedList<Node>();
//ทำการหาแบบ BFS
//ปริ๊นค่าผลลัพท์ว่าหาเจอหรือเปล่า
}
เราก็เขียน method BFS ขึ้นมา โดยเราจะต้องกำหนดค่าเริ่มต้นก่อน ซึ่งตัวที่เราจะต้องใช้เป็นดังนี้
- ค่า sum เพื่อเก็บว่าเส้นทางที่ผ่านมาเรามีผลรวมเป็นเท่าไหร่
- path (เป็น ArrayList) เอาไว้เก็บว่า Node ไหนที่เราเดินผ่านมาแล้วบ้าง
- next เป็น queue เอาไว้เก็บว่า Node ที่เราควรจะหาเป็นตัวถัดไปเป็นตัวไหน
*สำหรับ Java นั้นมีคลาส Queue ให้เรียกใช้อยู่แล้ว (เอ่อ จริงๆ ไม่แค่ Queue หรอกนะ Stack และ Tree มันก็มีให้ใช้ = =" )
แต่ จะเรียกมันว่า class ก็ไม่ถูกต้องเรียกว่า interface มากกว่า เพราะรูปแบบการสร้าง Queue ต้องเลือกว่าเราจะให้ Queue ของเราใช้รูปแบบไหนในการเก็บ ซึ่งตัวอย่างนี้เลือกใช้รูปแบบ LinkedList (แต่ไม่ว่าเราจะใช้โครงสร้างแบบไหน มันก็เป็นวิธีการที่ Queue จะจัดการให้โดยเราไม่ต้องสนใจมันก็ได้นะ)
เราใช้ Queue ในการหาแบบ BFS เพราะการ search หาทีละชั้นสามารถคุมได้ด้วย Queue
ตัวอย่างเช่น .. จาก Tree รูปข้างบน
เราหา (13) เป็นตัวแรก child ของ (13) นั้นมี 2 ตัวคือ (7) กับ (25) เราก็เอา (7)(25) ใส่ Queue ไว้
Queue: (7) (25)
ดังนั้นเมื่อเราต้องการรู้ว่า Node ต่อไปเราจะไปไหนต่อดี เราก็จะจัดการ poll ข้อมูลออกมาจาก Queue
(7) <-- Queue: (25)
เรา จะได้ว่า (7) คือตัวต่อไปที่เราจะต้องไป visit แล้วก็ทำเหมือนเดิมคือเมื่อเรามาถึง (7) แล้วก็จัดการเอา child ทุกตัวของมันใส่เข้าไปใน Queue จะได้ประมาณนี้
Queue: (25) (3) (10)
พอจะไปตัวต่อไปก็ทำเช่นเดิมคือ poll ข้อมูลออกมา
(25) <-- Queue: (3) (10)
เราก็ไป visit ที่ Node นั้น .. แล้วก็ทำแบบนี้ไปเรื่อยๆ เรื่อยๆ เรื่อยๆ นะ (ฮา)
อันดับต่อไปเราก็จะเริ่มทำการวนหา Node ที่มีค่า .data เท่ากับ value ที่เรารับมาตอนแรก
Node cur = root;
while (cur != null && cur.data != value) {
sum += cur.data;
path.add(cur);
next.add(cur.leftChild);
next.add(cur.rightChild);
cur = next.isEmpty() ? null : next.poll();
}
ในขั้นแรก เราสร้าง cur (current) ขึ้นมาเพื่อเอาไว้เก็บว่าตอนนี้เราหาถึงตอนไหนแล้ว
และเลือกใช้ while loop เพราะไม่รู้ว่ามันต้องใช้กี่ครั้งกว่าจะหาเจอ และใส่เงื่อนไขว่าเราจะทำการหาต่อไปถ้า..
- Node ที่เรากำลังหามาถึงในตอนนี้ ไม่ใช่ null (หมายความว่ายังมี Node ให้หาอยู่)
- data ของ Node ตัวที่เราหาอยู่ยังไม่ตรงกับ value ที่จะหา (ยังไม่ตรงก็หาไปเรื่อยๆ ไงล่ะ)
โดยในแต่ละรอบต้องทำการ บวกค่าของ Node ที่เดินทางผ่านมาเข้าไปใน sum และ เพิ่ม Node ตัวนั้นเข้าไปใน path และจบด้วยการที่เอา leftChild กับ rightChild ใส่ลงไปใน queue ซะ
ส่วนบรรทัดสุดท้ายนั้นคือการ อัพเดต current Node เป็นตัวถัดไป (ดึงออกมาจาก queue) และใช้เงื่อนไขว่า ถ้า queue ไม่มีข้อมูลให้ดึงมาใช้แล้ว (.isEmpty) ตัว cur ของเราจะมีค่าเป็น null แต่ถ้ายังดึงได้ก็จัดการดึงออกมา (.poll)
*บรรทัดสุดท้ายเป็นรูปย่อของการเขียนแบบ
if(next.isEmpty()){
cur = null;
}
else{
cur = next.poll();
}
หลังจากหาเสร็จ เราก็เช็กว่า cur != null หรือเปล่า ถ้ามันไม่เป็น null ก็แปลว่าเราหาเจอ เราก็ปริ๊นค่าผลลัพท์ออกไป เป็นอันจบ
if (cur != null) {
System.out.println("Found: " + value);
System.out.println("Sum: " + sum);
System.out.print("Path: ");
for (Node p : path) {
System.out.print(p.data + " ");
}
System.out.println();
}
else {
System.out.println("Not Found: " + value);
System.out.println("Sum: 0");
}
method DFS
public void DFS(int value) {
int sum = 0;
ArrayList<Node> path = new ArrayList<Node>();
Stack<Node> trackback = new Stack<Node>();
//เซ็ตให้ Node ทุกตัวมี status เป็น visited = false คือยังไม่เคยเดินผ่านมา
//ทำการหาแบบ DFS
//ปริ๊นค่าผลลัพท์ว่าหาเจอหรือเปล่า
}
ในการทำ DFS นั้นมีขั้นตอนคร่าวๆ คล้ายๆ กับ BFS แต่ต้องเพิ่มขั้นตอนในการเซ็ตค่าเพื่อบอกว่า Node
ใน Tree ต้นนี้ยังไม่เคยค้นหาผ่านมาก่อน (เริ่มแรกต้องยังไม่มี Node ตัวไหนเคยผ่านมาก่อนอยู่แล้วล่ะ)
และ การหาแบบ BFS เราใช้ queue แต่ถ้าเป็น DFS เราจะใช้ stack แทนเพื่อเก็บว่าทางที่ผ่านมาของเราเป็นตัวอะไร จะได้ย้อนกลับทางเดิมได้ถูก
Node cur = root;
while (cur != null && cur.data != value) {
if (!cur.visited) {
sum += cur.data;
path.add(cur);
}
cur.visited = true;
//จัดการเขยิบไป Node ที่ควรหาเป็นตัวถัดไปนะ
}
เงื่อนไขก็คล้ายๆ ของเดิมล่ะนะ สำหรับ BFS เราเริ่มโดยการ เพิ่มค่าเข้าไปใน sum และบันทึกเข้าไปใน path ที่ผ่านมา
แต่ สำหรับ DFS นั้นไม่สามารถทำแบบนั้นได้ เราต้องเช็กดูก่อนว่า Node ตัวนั้นยังไม่เคยผ่านมาก่อนถึงจะทำการบันทึกได้ (ถ้ามันผ่านมาแล้ว ก็ไม่ต้องบันทึกเพราะมันเคยบันทึกไปก่อนหน้านี้แล้วนะ)
แล้วก็ตบท้ายด้วยการเซ็กให้ Node ตัวที่กำลังหาอยู่กลายเป็น visited คือเคยผ่านมาแล้ว ไม่ต้องเอามาคิดอีก
หลังจากนั้นเป็นสเต็ปการ "เขยิบไปตัวถัดไป" ซึ่งแยกได้เป็น 3 กรณีคือ..
- child ทางซ้าย/ขวา ยังลงไปหาต่อได้
- ไปต่อไปไม่ได้ต้องย้อนกลับไปทางเก่า (กลับไปหา parent)
- กรณีสุดท้ายคือไปต่อไม่ได้ ถอยกลับก็ไม่ได้ null มันซะเลย
if (cur.leftChild != null && !cur.leftChild.visited) {
trackback.push(cur);
cur = cur.leftChild;
}
else if (cur.rightChild != null && !cur.rightChild.visited) {
trackback.push(cur);
cur = cur.rightChild;
}
else if (!trackback.isEmpty()) {
Node parent = trackback.pop();
cur = parent;
}
else {
cur = null;
}
ขั้นแรกเราก็เช็กว่าถ้าเราจะลงไปทางซ้ายเพื่อไปต่อ ก็ต้องเช็กว่ามี leftChild และ Node ต่อไปนั้นไม่เคยผ่านมาก่อนถึงจะลงไปได้
และ เพื่อให้รู้ว่าขากลับเราจะกลับทางไหน เราก็ต้องเพิ่ม Node ที่เราอยู่ในตอนนี้ใส่ใน trackback เพื่อตามรอยย้อนกลับได้แล้วจึงเขยิบลงไปทาง leftChild
*การเช็กฝั่ง rightChild ก็ทำแบบเดียวกัน
แต่ ถ้าลงไปไม่ได้ทั้งฝั่งซ้ายและฝั่งขวา เราก็จะย้อนกลับไปทางเดิมเพื่อหาว่ามีทางไหนที่ไปต่อได้อีกรึเปล่า วิธีการก็ไม่ยากหรอกแค่ pop ข้อมูลออกมาจาก trackback ก็จะรู้ว่าตัว parent ของมันต้องย้อนกลับไปไหนแล้ว
แต่ก่อนจะ pop ข้อมูลออกมาเราต้องเช็กก่อนว่า stack มีข้อมูลให้ pop รึเปล่าด้วยคำสั่ง isEmpty ถ้าไม่เหลืออะไรแล้วก็แปลว่า null เลย
แล้วสเต็ปสุดท้ายก็ปริ๊นผลออกไปด้วยโค้ดชุดเดียวกับ BFS เลย
เขียน main เพื่อสั่งงาน class ที่เขียนมาแล้ว
เราจะใช้ method readfile จากงานที่แล้ว http://nartra.blogspot.com/2013/10/project-solution-queue-step-by-step.html ในการอ่านไฟล์ input
static final int BFS = 1, DFS = 2;
public static void main(String[] args) {
String[] cmd = readFile("input.txt");
//first line
String[] inputStr = cmd[0].split(" ");
int i;
int[] inputInt = new int[inputStr.length];
for (i = 0; i < inputInt.length; i++) {
inputInt[i] = Integer.parseInt(inputStr[i]);
}
Tree tree = new Tree();
//ใส่เลขแต่ละตัวเข้าไป Tree
for (i = 0; i < inputInt.length; i++) {
tree.add(inputInt[i]);
}
//บรรทัดต่อไปอ่านมาทีละคำสั่งโดยมี typeOfCommand เป็นตัวเช็กให้ว่ามันเป็นรูปแบบคำสั่งแบบ BFS หรือ DFS
}
เราก็เขียน main ขึ้นมาแล้วอ่านไฟล์คำสั่งเข้ามา
ในบรรทัดแรกมันคือข้อมูลที่เราจะใส่เข้าไปใน Tree เราก็ใช้ .split เพื่อตัดตัวเลขออกเป็นชิ้นเลขย่อยๆ แล้ว add เข้าไปใน Tree
เราจะใช้ method typeOfCommand จากงานที่แล้ว http://nartra.blogspot.com/2013/10/project-solution-queue-step-by-step.html อีกเช่นเคยแต่เปลี่ยนรูปแบบของ Regular Expression เป็น
static int typeOfCommand(String str) {
str = str.trim();
String BFS_format = "^(BFS)\\([0-9]+\\)$";
String DFS_format = "^(DFS)\\([0-9]+\\)$";
Pattern pattern;
Matcher matcher;
pattern = Pattern.compile(BFS_format);
matcher = pattern.matcher(str);
if (matcher.find()) {
return BFS;
}
pattern = Pattern.compile(DFS_format);
matcher = pattern.matcher(str);
if (matcher.find()) {
return DFS;
}
return UNKNOWN;
}
แต่ เราจะเพิ่ม method ตัวช่วยอีกตึวนึงเพื่อเอาไว้หาค่าว่า String ตัวนี้มีค่าเลขเป็นอะไร (ตัดทุกอย่างที่ไม่ใช่ตัวเลขทิ้ง แล้ว parseInt ซะ)
static int getValue(String str) {
return Integer.parseInt(str.replaceAll("[^\\d]", ""));
}
มาถึงจุดนี้เราก็วนลูปเช็กตั้งแต่บรรทัดที่ 2 (เพราะบรรทัดแรกเป็น data สำหรับ input ไปแล้ว) จากนั้นก็เช็กด้วย typeOfCommand ว่า type เป็น BFS หรือ DFS
//บรรทัดต่อไปอ่านมาทีละคำสั่งโดยมี typeOfCommand เป็นตัวเช็กให้ว่ามันเป็นรูปแบบคำสั่งแบบ BFS หรือ DFS for (i = 1; i < cmd.length; i++) { switch (typeOfCommand(cmd[i])) { case BFS: tree.BFS(getValue(cmd[i])); break; case DFS: tree.DFS(getValue(cmd[i])); break; } }
จากนั้นก็สั่งให้ tree ของเราค้นหาเลขตัวนั้นตามแบบ BFS หรือ DFS เป็นอันจบ
* ขอไม่รวม code ให้ละกัน ลองอ่านตามดูแล้วทำไปเรื่อยๆ step by step