บทความชุด: Functional Programming
รวมเนื้อหาเกี่ยวกับการเขียนโปรแกรมแนว Functional และหัวข้ออื่นๆ ที่เกี่ยวข้อง
- ตอนที่ 1 Pure, First-Class, High-Order, พื้นฐานแห่ง Functional Programming
- ตอนที่ 2 Lambda Function and Closure ฟังก์ชันทันใจและพื้นที่ปิดล้อม!
- ตอนที่ 3 map filter reduce และเพื่อนๆ พระเอกแห่งโลก Functional
- ตอนที่ 4 โครสร้างแบบ Pair และ Either กับ List Comprehension การสร้างลิสต์ฉบับฟังก์ชันนอล
- ตอนที่ 5 Lazy Evaluation ขี้เกียจไว้ก่อนแล้วดีเอง?!
- ตอนที่ 6 Recursive Function ฟังก์ชันเวียนเกิด, เขียนลูปไม่ได้ทำยังไง? มาเขียนฟังก์ชันเรียกตัวเองแทนกันเถอะ!
- ตอนที่ 7 Curry, Partial Function
- ตอนที่ 8 Functor, Monad
- [บทความปี 2015] มารู้จักกับ Functional Programming สิ่งที่คุณต้องรู้ในตอนนี้กันเถอะ
- Function ทำงานยังไง?, ในมุมมองของโปรแกรมเมอร์สาย Imperative
Category Theory & Lambda Calculus
เนื้อหาเกี่ยวกับคณิตศาสตร์ในบทความนี้ได้รับคำปรึกษาและตรวจทานจาก muitsfriday.dev
ทฤษฎีแคตากอรีเป็นหนึ่งในสาขาของวิชา Mathematics ซึ่งเป็นแนวคิดที่ต่อมาถูกเอามาใช้เป็นหลักการออกแบบภาษาโปรแกรมคอมพิวเตอร์ ดังนั้นจะบอกว่าเป็นหัวข้อทางคณิตศาสตร์ที่ programmer ที่ไม่ได้มาจากสาย math สามารถเรียนรู้และทำความเข้าใจได้ง่ายเพราะคุ้นเคยกับมันอยู่นิดหน่อยแล้วก็ว่าได้
Concept
Category เป็นการประกอบกันของ 2 สิ่ง นั่นคือ
- Object
- Arrows (หรือ Morphism อ่านว่า "มอร์ฟิซึม")
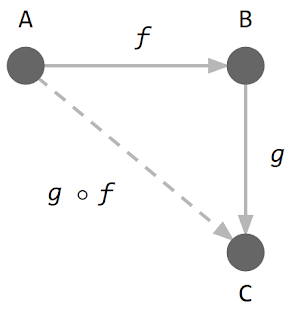
Object นั้นจะเป็นอะไรก็ได้ แต่ละ Object สามารถแปลงไปเป็นอีก Object หนึ่งได้ด้วยการเขียนลูกศร Arrow ลงไป
อย่างนี้ตัวอย่างข้างบนนี้ เรามี Object ชื่อ A ซึ่งแปลงไปเป็น B ได้ด้วย Arrow f (หรือ Morphism f) จากนั้นเราก็สามารถแปลง B ให้กลายเป็น C ได้ด้วย Arrow g อีกทีหนึ่ง
จากนิยามแค่นี้ น่าจะไม่เข้าใจและไม่เห็นภาพแน่นอน งั้นมาดูตัวอย่างกัน
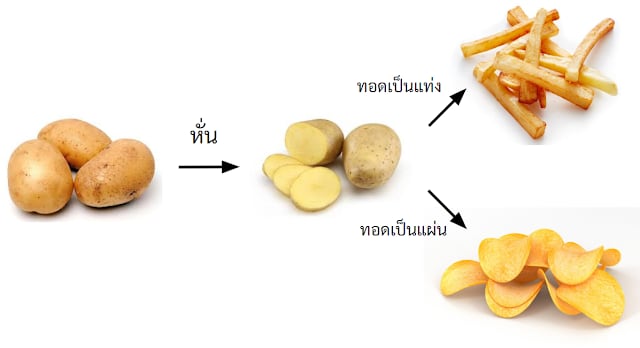
สมมุติว่า Category ของเราเป็นโลกแห่ง "มันฝรั่ง" เราอาจจะสร้าง Category ได้ประมาณนี้
- Object: มันฝรั่งแบบเป็นลูก, มันฝรั่งหั่น, เฟรนฟราย, มันฝรั่งแผ่นทอด
- Arrow: การหั่น, การทอด
ป.ล. จริงๆ มันต้องหั่นเป็นแผ่น หรือ หั่นเป็นแท่ง แล้วค่อย --> ทอดนะ ...แต่หารูปประกอบไม่ได้!! (ฮา)
แล้วเรื่องนี้มันเกี่ยวอะไรกับการเขียนโปรแกรมด้วย คงสงสัยกันอยู่ละสิ! นั่นก็คือ...
Category of Type
สำหรับโลก Programming, ถ้าในมุมมอง Category แล้วเราจะมองมันเป็น Category of Type คือเป็นกลุ่มของตัวแปรชนิดต่างๆ มารวมกัน ไม่ว่าจะเป็น int, double, string, boolean อะไรพวกนั้น
ส่วน Arrow ก็คือ function ในโปรแกรมมิ่งนั่นเอง เพราะฟังก์ชันจะรับตัวแปร (เทียบกับ object) เข้าไป แล้วคายตัวแปรอีกแบบกลับมา เช่น สร้างฟังก์ชันที่รับ int และ return string กลับมาอะไรแบบนั้น
Compose
คอมโพสแปลได้ว่า "การประกอบเข้าด้วยกัน" ในเชิงของ Category ถ้าเรามีความสัมพันธ์ A --> B --> C แล้วเราสามารถสร้างทางลัดตรงจาก A --> C ได้เลย เรียกว่าการ "Compose" นั่นเอง
แล้วถ้าเรามองว่า f เป็นฟังก์ชันสำหรับแปลง A --> B และ g เป็นฟังก์ชันแปลงจาก B --> C ถ้าเขียนเป็นโค้ดก็จะได้แบบนี้
B = f(A)
C = g(B)
ถ้าเราจะทำการ compose สองฟังก์ชันนี้เข้าด้วยกันก็จะเขียนได้ว่า
C = g(f(A))
หรือเขียนแบบคณิตศาสตร์จะได้
C = (g ∘ f)(A) //อ่านว่า "g of f" หรือ "g after f"
note: การ compose ฟังก์ชันในคณิคศาสตร์จะคล้ายๆ กับการเขียน "Pipeline" ในโลกโปรแกรมมิ่ง
A |> f |> gหรือ
A |> a => f(a) |> b => g(b)ข้อแตกต่างที่ควรระวังคือ (g ∘ f) หมายถึงทำงาน
f->gนั่นคือทำงานจากฟังก์ชันข้างหลังก่อนคือเรียง ขวาไปซ้าย แต่ถ้าเขียนแบบ pipeline การทำงานจะเป็นแบบอ่านตามลำดับคือ ซ้ายไปขวา/บนลงล่างnote: ฟีเจอร์การเขียน pipeline ไม่ได้มีในทุกภาษา ตรวจสอบก่อนใช้งานด้วย
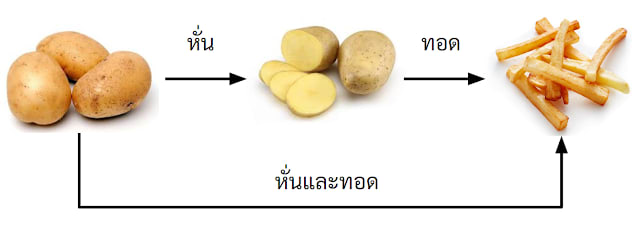
ถ้ากลับไปที่โลกมันฝรั่งของเรา ก็อาจจะสร้าง Arrow เพิ่มได้แบบนี้
แล้ว Category มีกฎอะไรอีกบ้างนะ?
อะไรจะถือว่าเป็น Category บ้างมีกฎง่ายๆ (แต่ก็ไม่ง่าย! เอ๊ะ ยังไง?) อยู่ 2 ข้อคือ...
- Composition Associative
- Identity Arrow
Composition Associative: คุณสมบัติการเปลี่ยนกลุ่ม
ก่อนอื่นก็ต้องมีคุณสมบัติการสลับที่ เรื่องนี้เป็นเรื่องเดียวกับการสลับที่ในวิชาเลขนั่นแหละ แบบนี้
(1 x 2) x 3 = 1 x (2 x 3)
นั่นคือถ้าเรามี Category A, B, C, D อยู่ตามภาพนี้

เราเริ่มต้นด้วยการมี Arrow 3 ตัวคือ f, g, และ h เราสามารถเอาทั้งหมดมาต่อ/ผสมกันได้แบบนี้
h ∘ g ∘ f
= h ∘ (g ∘ f)
= (h ∘ g) ∘ f
นั่นคือไม่ว่าเราจะทำฟังก์ชันไหนก่อน ก็จะได้ผลลัพธ์ออกมาเหมือนกัน (แต่สลับลำดับไม่ได้นะ เช่นจะเรียงแบบ g ∘ h ∘ f นี้ไม่ได้)
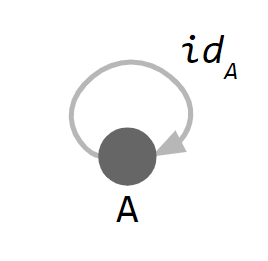
Identity Arrow: คุณสมบัติการมีเอกลักษณ์
ทุกๆ Object จะต้องมี Arrow ที่วิ่งกลับเข้าหาตัวเองเสมอ แบบนี้
หากเราเอา Identity Arrow ตัวนี้ไปทำการ compose กับ Arrow ตัวอื่น ผลลัพธ์จะได้ Arrow ตัวนั้นเสมอ (เสมือนว่า Arrow ตัวที่เป็น Identity นั้นจะหายไปเลย)
แบบนี้
{id} ∘ f = f
f ∘ {id} = f
หรือถ้าเขียนเป็นโปรแกรมมิ่งก็จะได้ว่า
function identity(x){
return x;
}
หรือถ้าใช้ภาษาโปรแกรมสไตล์ FP ก็จะได้แบบนี้
identity :: A => A
identity x = x
ต่อไปมาดูตัวอย่างกันหน่อย
สมมุติเรามี array อยู่หนึ่งตัว ถ้าเราจะสร้าง identity ขึ้นมาก็จะได้แบบนี้
[1, 2, 3, 4] ++ [] = [1, 2, 3, 4]
[] ++ [1, 2, 3, 4] = [1, 2, 3, 4]
concat หรือการ "ต่อ array" ก็จะมี "Empty Array" (อะเรย์ว่าง) เป็นเอกลักษณ์ของ array เพราะไม่ว่าเราจะเอา empty array ไปต่อกับ array ตัวไหนก็ตามจะได้ array ตัวเดิมเสมอ
note: สัญลักษณ์ concat ที่ใช้ในตัวอย่างใช้ ++ ซึ่งแต่ละภาษาโปรแกรมก็อาจจะมีวิธีเขียนที่ต่างกัน เช่นบางภาษาอาจจะใช้ +, :, .concat(), .extend(), หรือ .merge() แทน
ถ้า array ยากไปลองมาดูตัวที่ง่ายขึ้นอีกนิด กับ Int
x + 0 = x
0 + x = x
+0 เป็นเอกลักษณ์ของตัวเลข ไม่ว่าจะเอาไปบวกกับอะไรก็ได้เลขตัวเดิมเสมอ
หรืออาจจะใช้การคูณแบบนี้
x * 1 = x
1 * x = x
แบบนี้ก็ได้นะ (identity ไม่จำเป็นต้องมีแค่ตัวเดียว)
เพราะ *1 ก็เป็นเอกลักษณ์ของตัวเลขเช่นกัน
แต่ก็ต้องอธิบายเพิ่มเติมว่าการบอกแบบนี้ได้ จะต้องกำหนดว่า category ของเราเป็น Category of Integer เท่านั้นนะ!
เพราะถ้าเรากำหนด category ของเราเป็น Category of Type เช่นชนิดตัวแปรในภาษาโปรแกรม เราจะได้ว่าไม่ว่าจะเอาตัวเลขตัวไหนมาบวกหรือคูณกันก็ถือเป็นเอกลักษณ์ทั้งนั้น (ไม่เข้าใจเหรอ งั้นมาดูตัวอย่างต่อ)
1 + 2 = 3
7 - 6 = 1
4 * 5 = 20
แบบนี้ถือว่าเป็น identity ได้ทั้งหมด เพราะไม่ว่าเราจะเอาไปทำ operation ตัวไหนก็ได้ผลออกมาเป็นค่าเดิม! เพราะว่า...
Int + Int = Int
Int - Int = Int
Int * Int = Int
เพราะถ้าเราโฟกัสที่ Type ไม่ว่าจะเป็น 1, 2, 3 ก็จัดเป็น Int ทั้งนั้น
และเช่นกันนะ ถ้าในมุมมองของ Category of Type การ concat array เมื่อกี้นี้ก็ไม่จำเป็นต้องเป็น Empty Array เท่านั้นนะ จะเอาarrayตัวไหนมาconcatกันก็ถือว่าเป็น identity ทั้งนั้น เพราะ
สรุป
ในบทความนี้เป็นการแนะนำเนื้อหา Category Theory แบบคร่าวๆ มากๆ ซึ่งพื้นฐานคอนเซ็ปในการเอาไปศึกษาต่อในเรื่องของ Functional Programming
แต่ถ้าอ่านมาจนถึงตอนนี้อาจจะยังไม่เห็นภาพชัดเจน (ก็คือยังไม่รู้นั่นแหละว่าเราจะเอาไป apply กับการเขียนโปรแกรมได้ยังไง) เพราะว่ายังมีอีกหลายเรื่องที่ต่อจากนี้ ไม่ว่าจะเป็น functor, ord, monad ซึ่งเรื่องพวกนี้ถูกเอาไปใช้เป็นคอนเซ็ปของการออกแบบภาษาโปรแกรมสาย Functional Programming (FP) เลย ถ้าเรารู้พื้นฐานพวกนี้ดี การศึกษา FP ก็จะไปได้เร็วมากขึ้น








ขอบคุณที่เขียนบทความเกี่ยวกับ category thoery นะครับ ผมหวังว่าคนไทยเราจะใช้มันกันมากขึ้นเพราะมีประโยชน์จริงๆ
ว่าแต่รบกวนแก้ typo เกี่ยวกับ associativity นิดนึงนะครับ f . g ควรเป็น g . f, และ typo แบบเดียวในสำหรับ g . h, และ f . g . h นะครับ
ขอแถมนิดนึง ผมเข้าใจว่า composition มันจะงงๆเพราะว่า g . f คือมันผ่าน f ก่อน g ดังนั้นบางที่เรา จะใช้ f ; g := g . f เพื่อป้องกันความงง (สาเหตุที่ใช้ ; เพราะเหมือนกับตัวเชื่อมสองคำสั่งในภาษาซี) notation นี้ค่อนข้างจะเป็นมาตรฐานระดับหนึ่งเลยในทาง computer science
ดูดีมากครับ
เวลาอ่าน Haskell แล้วทำรู้สึกยาก ๆ หรือว่ามันยากที่ grammar ของ Haskell เองไม่ได้ยากเพราะ Category Theory